Universal Algebra

Mathematics is replete with examples of algebraic constructions such as groups, vector spaces, monoids, etc. The mathematical subject of Universal Algebra studies such algebraic constructions generically. This post is a collection of notes that I compiled a while ago while studying Universal Algebra. In these notes, I attempted to formulate Universal Algebra entirely in terms of category theory (it is often formulated in terms of set theory). Universal Algebra and category theory are closely related subjects and align quite naturally. One advantage of this formulation is that it permits the expression of algebraic concepts in categories other than the category of sets.

Algebras

Definition (Algebra). An algebra consists of an endofunctor \(\Sigma\) on a category \(\mathbb{C}\) called the signature, an object \(A\) of \(\mathbb{C}\) called the carrier, and a morphism \(f^A : \Sigma(A) \rightarrow A\) called the operation.

Notation (\(\Sigma\)-algebra). An algebra with signature \(\Sigma\) is often called a \(\Sigma\)-algebra.

Notation (Algebra Naming Convention). We adopt the convention that algebras are written in calligraphic typeface \(\mathcal{A}\) and the respective carrier is written in plain typeface \(A\) using the same letter, and the operation \(f^{\mathcal{A}}\) uses \(f\) with a superscript corresponding to the algebra.

Homomorphisms

Definition (Homomorphism of Algebras). A homomorphism from a \(\Sigma\)-algebra \(\mathcal{A}\) to a \(\Sigma\)-algebra \(\mathcal{B}\) is a morphism \(\phi : A \rightarrow B\) such that \(\phi \circ f^A = f^B \circ \Sigma(\phi)\), i.e. the following diagram commutes.

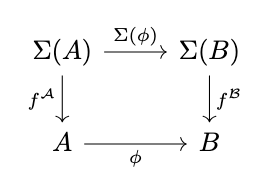
Categories of Algebras

Definition (Category of Algebras). The category of algebras \(\Sigma\)-Alg has \(\Sigma\)-algebras as its objects and \(\Sigma\)-algebra homomorphisms as its morphisms.

Notation (Homomorphism Domain and Codomain). The definition of a category of algebras implies that homomorphisms are morphisms in two categories. For a signature \(\Sigma\) on a category \(\mathbb{C}\), we will write \(\phi : \mathcal{A} \rightarrow \mathcal{B}\) when emphasizing the role of a homomorphism \(\phi\) as a morphism from an algebra \(\mathcal{A}\) to an algebra \(\mathcal{B}\) in \(\Sigma\)-Alg, and we will write \(\phi: A \rightarrow B\) when emphasizing the role of the same homomorphism as a morphism in the category \(\mathbb{C}\).

Subalgebras

Definition (Subalgebra). A subalgebra of a \(\Sigma\)-algebra \(\mathcal{A}\) is a \(\Sigma\)-algebra \(\mathcal{S}\) which admits a monomorphism \(\phi : \mathcal{S} \hookrightarrow \mathcal{A}\), i.e., the following diagram commutes. A subalgebra is a proper subalgebra if the respective monomorphism is not an isomorphism.

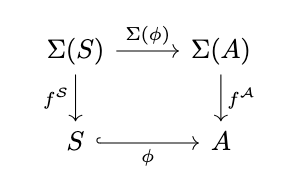
Initial Algebras

Definition (Initial Algebra). The initial algebra is the initial object \(\mathcal{I}[\Sigma]\) in \(\Sigma\)-Alg, i.e. for any \(\Sigma\)-algebra \(\mathcal{A}\), there exists a unique homomorphism \(\phi : \mathcal{I}[\Sigma] \rightarrow \mathcal{A}\), i.e., the following diagram commutes.

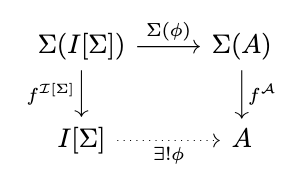
The Fixed Point Theorem

Theorem (Fixed Point). The carrier of an initial algebra is a fixed point of the respective signature.

Proof. Consider the following diagram.

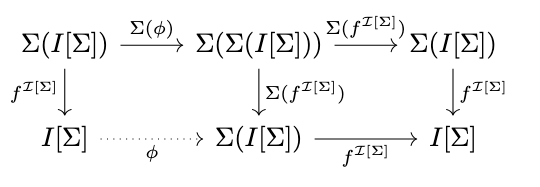
Thus, \(f^{\mathcal{I}[\Sigma]} \circ \phi\) is a homomorphism; however, \(1_{I[\Sigma]}\) is also a homomorphism, so \(f^{\mathcal{I}[\Sigma]} \circ \phi = 1_{I[\Sigma]}\). Likewise:

\begin{align*}
\phi \circ f^{\mathcal{I}[\Sigma]} &= \Sigma(f^{\mathcal{I}[\Sigma]}) \circ \Sigma(\phi) & \textrm{(\(\phi\) is a homomorphism)} \\
&= \Sigma(f^{\mathcal{I}[\Sigma]} \circ \phi) & \textrm{(Functoriality)} \\
&= \Sigma(1_{I[\Sigma]}) & \textrm{(By Previous Argument)} \\
&= 1_{\Sigma(I[\Sigma])} & \textrm{(Functoriality)}
\end{align*}

Thus, \(\Sigma(I[\Sigma]) \cong I[\Sigma]\). \(\square\)

Structural Induction

Theorem (Structural Induction). There are no proper subalgebras of an initial algebra.

Proof. Consider the following diagram.

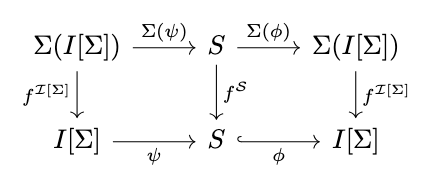
Since both inner squares commute, the outer square commutes, and thus \(\phi \circ \psi\) is a endomorphism on \(\mathcal{I}[\Sigma]\). However, the identity \(1_{I[\Sigma]}\) is also such an endomorphism, and thus, since \(\mathcal{I}[\Sigma]\) is initial, this endomorphism must be unique, so \(\phi \circ \psi = 1_{I[\Sigma]}\).

Next, consider the following diagram.

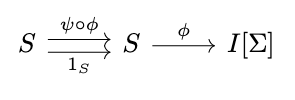
This diagram commutes, since:

\begin{align*}
\phi \circ (\psi \circ \phi) &= (\phi \circ \psi) \circ \phi & \textrm{(Associativity)} \\
&= 1_{I[\Sigma]} \circ \phi & \textrm{(Previous Argument)} \\
&= \phi & \textrm{(Identity)}
\end{align*}

Since \(\phi\) is a monomorphism, it follows that \(\psi \circ \phi = 1_S\). Thus, \(\phi\) is an isomorphism, and is improper. \(\square\)

Term Algebras

Notation (\(\Sigma_V\)). We will write \(\Sigma_V\) for the functor \(\Sigma(-) + V\), i.e. the functor defined as \(\Sigma_V(X) = \Sigma(X) + V\) for objects and \(\Sigma_V(f) = \Sigma(f) + 1_V\) for arrows, i.e. the coproduct \(\Sigma + \mathbf{1}_V\) of \(\Sigma\) and the constant functor \(\mathbf{1}_V\).

Definition (Term Algebra). The term algebra \(\mathcal{T}[\Sigma, V]\) for a signature \(\Sigma\) and object of variables \(V\) is the \(\Sigma\)-algebra with carrier \(T[\Sigma, V] = I[\Sigma_V]\) and operation \(f^{\mathcal{T}[\Sigma, V]} = f^{\mathcal{I}[\Sigma_V]} \circ i\), where \(i : \Sigma(I[\Sigma_V]) \rightarrow \Sigma(I[\Sigma_V]) + V\) is the respective coproduct injection.

Free Algebras

Definition (Forgetful Functor).

The forgetful functor \(U : \Sigma\textrm{-}Alg \rightarrow \mathbb{C}\) maps each algebra to its carrier and each homomorphism to itself (as an object of \(\mathbb{C}\)).

Definition (Free Algebra). The free algebra \(\mathcal{F}[\Sigma, V]\) for a signature \(\Sigma\) and object of variables \(V\) is the free object in \(\Sigma\)-Alg relative to the forgetful functor \(U\), i.e. there exists a morphism \(\eta_V : V \rightarrow F[\Sigma, V]\) called the insertion of generators (or insertion of variables) such that for any algebra \(\mathcal{A}\) and morphism \(f : V \rightarrow A\), there exists a unique homomorphism \(\phi_f : \mathcal{F}[\Sigma, V] \rightarrow \mathcal{A}\) such that \(\phi_f \circ \eta_V = f\), i.e., the following diagram commutes.

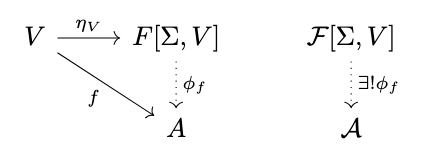
Theorem. Every term algebra is a free algebra.

Proof. Define \(\eta_V = f^{\mathcal{I}[\Sigma_V]} \circ i_V\). Let \(f : V \rightarrow A\) be any morphism for some algebra \(\mathcal{A}\). Consider diagram the following diagram in \(\Sigma_V\)-Alg.

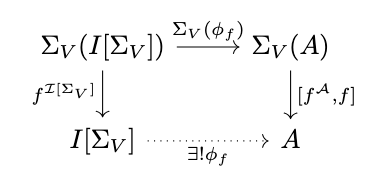
Since \(\mathcal{I}[\Sigma_V]\) is the initial algebra, there exists a unique homomorphism \(\phi_f\) that makes this diagram commute. Now consider the following diagram in \(\Sigma\)-Alg.

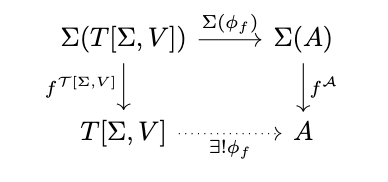
This diagram commutes, since:

\begin{align*}
\phi_f \circ f^{\mathcal{T}[\Sigma, V]} &= \phi_f \circ f^{\mathcal{I}[\Sigma_V]} & \textrm{(By definition of \(f^{\mathcal{T}[\Sigma, V]}\))} \\
&= ([f^{\mathcal{A}}, f] \circ \Sigma(\phi_f) + 1_V) \circ i & \textrm{(By definition of \(\phi_f\))} \\
&= [f^{\mathcal{A}} \circ \Sigma(\phi_f), f] \circ i & \textrm{(By theorem XXX)} \\
&= f^{\mathcal{A}} \circ \Sigma(\phi_f) & \textrm{(By definition of coproduct)}
\end{align*}

Finally, consider the following diagram.

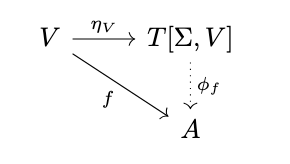
This diagram commutes, since:

\begin{align*}
\phi_f \circ \eta_V &= \phi_f \circ f^{I[\Sigma_V]} \circ i & \textrm{(By definition of \(\eta_V\))} \\
&= ([f^{\mathcal{A}}, f] \circ \Sigma(\phi_f) + 1_V) \circ i & \textrm{(By definition of \(\phi_f\))} \\
&= [f^{\mathcal{A}} \circ \Sigma(\phi_f), f] \circ i & \textrm{(By theorem XXX)} \\
&= f & \textrm{(By definition of coproduct)}
\end{align*}

Now, suppose that there exists another homomorphism \(\phi_f' : \mathcal{T}[\Sigma, V] \rightarrow \mathcal{A}\) such that \(\phi_f' \circ \eta_V = f\). Then:

\begin{align*}
\phi_f' \circ f^{\mathcal{I}[\Sigma_V]} &= [f^{\mathcal{A}} \circ \Sigma(\phi_f'), f] & \textrm{(Since \(\phi_f' \circ f^{\mathcal{I}[\Sigma_V]} \circ i_\Sigma = f^{\mathcal{A}} \circ \Sigma(\phi_f)\) and \(\phi' \circ f^{\mathcal{I}[\Sigma_V]} \circ i_V = f\))} \\
&= [f^{\mathcal{A}} \circ \Sigma(\phi_f'), f \circ 1_V] & \textrm{(Identity)} \\
&= [f^{\mathcal{A}}, f] \circ (\Sigma(\phi_f') + 1_V) & \textrm{(Theorem XXX)} \\
&= [f^{\mathcal{A}}, f] \circ \Sigma_V(\phi_f') & \textrm{(By definition of \(\Sigma_V\))}
\end{align*}

Since \(\mathcal{I}[\Sigma_V]\) is an initial algebra, \(\phi_f' = \phi_f\). \(\square\)

Theorem. Every free algebra is a term algebra.

Proof. For a free algebra \(\mathcal{F}[\Sigma, V]\), consider an arbitrary \(\Sigma_V\)-algebra \(\mathcal{A}\) as in the following diagram.

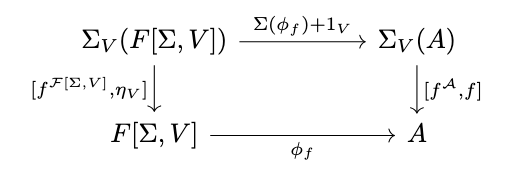
Next, observe that:

\begin{align*}
\phi_f \circ [f^{\mathcal{F}[\Sigma, V]}, \eta_V] &= [\phi_f \circ f^{\mathcal{F}[\Sigma, V]}, \phi_f \circ \eta_V] & \textrm{(By Definition of Coproduct)} \\
&= [f^{\mathcal{A}} \circ \Sigma(\phi_f), f] & \textrm{(Homomorphism, Definition of \(\eta_V\))} \\
&= [f^{\mathcal{A}}, f] \circ (\Sigma(\phi_f) + 1_V) & \textrm{(Definition of Coproduct)}
\end{align*}

Thus, \(\phi_f\) is a \(\Sigma_V\)-homomorphism. Suppose that there exists another such homomorphism \(\phi_f'\). Then, since

\begin{align*}
\phi_f' \circ [f^{\mathcal{F}[\Sigma, V]}, \eta_V] &= [f^{\mathcal{A}}, f] \circ (\Sigma(\phi_f') + 1_V) & \textrm{(\(\phi_f'\) is a homomorphism)} \\
\end{align*}

it thus follows that:

\begin{align*}
[\phi_f' \circ f^{\mathcal{F}[\Sigma, V]}, \phi_f' \circ \eta_V] &= [f^{\mathcal{A}} \circ \Sigma(\phi_f'), f]
\end{align*}

and thus \(\phi_f' \circ f^{\mathcal{F}[\Sigma, V]} = f^{\mathcal{A}} \circ \Sigma(\phi_f')\) and \(\phi_f' \circ \eta_V = f\). Since \(\mathcal{F}[\Sigma, V]\) is a free algebra, \(\phi' = \phi\). Since \([f^{\mathcal{F}[\Sigma, V]}, \eta_V] \circ i_\Sigma = f^{\mathcal{F}[\Sigma, V]}\), it follows that \(\mathcal{F}[\Sigma, V]\) is a term algebra. \(\square\)

Theorem (Construction of Free Algebras). For any category \(\mathbb{C}\) which has all directed colimits and signature \(\Sigma\) on \(\mathbb{C}\) which preserves all directed colimits, there exists a free algebra \(\mathcal{F}[\Sigma, V]\) for every object \(V\) of \(\mathbb{C}\).

Proof. The index category \(\omega\) is defined as follows:

• Objects: natural numbers \(n \in \mathbb{N}\),
• Arrows: \(f : m \rightarrow n\) iff \(m \leq n\).

The diagram \(D: \omega \rightarrow \mathbb{C}\) is defined as follows:

• Objects:
  • \(D(0) = V\),
  • \(D(n+1) = \Sigma_V(D(n))\),
• Arrows:
  • \(D(0 \leq 0) = 1_V\),
  • \(D(0 \leq n+1) = i_V : V \rightarrow \Sigma_V^n(V)\),

\(D(m+1 \leq n+1) = \Sigma_V(D(m \leq n))\).

Consider the following diagram.

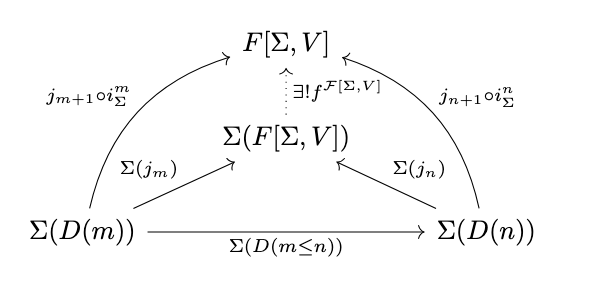
The outer triangle of this diagram commutes, since:

\begin{align*}
(j_{n+1} \circ i_\Sigma^n) \circ \Sigma(D(m \leq n)) &= j_{n+1} \circ (i_\Sigma^n \circ \Sigma(D(m \leq n))) & \textrm{(Associativity)} \\
&= j_{n+1} \circ (D(m+1 \leq n+1) \circ i_\Sigma^m) & \textrm{(x)} \\
&= (j_{n+1} \circ D(m+1 \leq n+1)) \circ i_\Sigma^m & \textrm{(Associativity)} \\
&= j_{m+1} \circ i_\Sigma^m & \textrm{(Cocone)}
\end{align*}

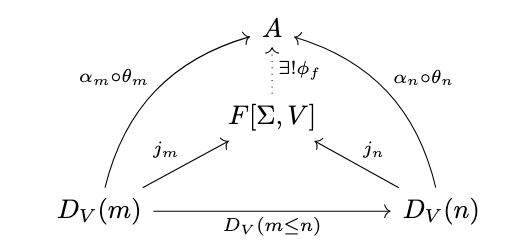
Thus, since \(\Sigma\) preserves directed colimits, the inner triangle commutes and there exists a unique morphism \(f^{\mathcal{F}[\Sigma, V]} : \Sigma(F[\Sigma, V]) \rightarrow F[\Sigma, V]\) that makes the diagram commute. Thus, there exists an algebra with signature \(\Sigma\), carrier \(F[\Sigma, V]\), and operation \(f^{\mathcal{F}[\Sigma, V]}\).

Consider any algebra \(\mathcal{A}\) and morphism \(f : V \rightarrow A\). Define a family of morphisms as follows:

• \(\theta_0 = f\),
• \(\theta_{n+1} = \Sigma(\theta_n) + f\).

Next, define a family of morphisms as follows:

• \(\alpha_0 = 1_A\),
• \(\alpha_{n+1} = [f^{\mathcal{A}} \circ \Sigma(\alpha_n), 1_A]\).

This induces a homomorphism \(\phi_f\), as shown in the following diagram.

When \(m = 0\) and \(n = 0\):

\begin{align*}
(\alpha_n \circ \theta_n) \circ D_V(m \leq n) &= (\alpha_0 \circ \theta_0) \circ D_V(0 \leq 0) & \textrm{(Inductive Hypothesis)} \\
&= (\alpha_0 \circ \theta_0) \circ 1_V & \textrm{(Definition of \(D_V(0 \leq 0)\))} \\
&= \alpha_0 \circ \theta_0 & \textrm{(Identity)} \\
&= \alpha_m \circ \theta_m & \textrm{(Inductive Hypothesis)}
\end{align*}

When \(m = 0\) and \((\alpha_n \circ \theta_n) \circ D_V(0 \leq n) = \alpha_0 \circ \theta_0\):

\begin{align*}
(\alpha_{n+1} \circ \theta_{n+1}) \circ D_V(m \leq n+1) &= (\alpha_{n+1} \circ \theta_{n+1}) \circ D_V(0 \leq {n+1}) & \textrm{(Inductive Hypothesis)} \\
&= ([f^{\mathcal{A}} \circ \Sigma(\alpha_n), 1_A] \circ (\Sigma(\theta_n) + f)) \circ D_V(0 \leq {n+1}) & \textrm{(Inductive Hypothesis)} \\
&= ([f^{\mathcal{A}} \circ \Sigma(\alpha_n), 1_A] \circ (\Sigma(\theta_n) + f)) \circ i_V^n & \textrm{(By definition)} \\
&= [(f^{\mathcal{A}} \circ \Sigma(\alpha_n)) \circ \Sigma(\theta_n), 1_A \circ f] \circ i_V^n & \textrm{(By definition)} \\
&= 1_A \circ f &\textrm{(By definition)} \\
&= \alpha_0 \circ \theta_0 & \textrm{(By definition)} \\
&= \alpha_m \circ \theta_m & \textrm{(Inductive Hypothesis)}
\end{align*}

When \((\alpha_n \circ \theta_n) \circ D_V(m \leq n) = (\alpha_m \circ \theta_m)\):

\begin{align*}
(\alpha_{n+1} \circ \theta_{n+1}) \circ D_V(m+1 \leq n+1) &= ([f^{\mathcal{A}} \circ \Sigma(\alpha_n), 1_A] \circ (\Sigma(\theta_n) + f)) \circ (\Sigma(D_V(m \leq n)) + 1_V) & \textrm{(By definition)} \\
&= ([(f^{\mathcal{A}} \circ \Sigma(\alpha_n)) \circ \Sigma(\theta_n) , 1_A \circ f] \circ (\Sigma(D_V(m \leq n)) + 1_V) \\
&= [((f^{\mathcal{A}} \circ \Sigma(\alpha_n)) \circ \Sigma(\theta_n)) \circ \Sigma(D_V(m \leq n)), 1_A \circ f \circ 1_V] \\
&= [(f^{\mathcal{A}} \circ (\Sigma(\alpha_n) \circ \Sigma(\theta_n))) \circ \Sigma(D_V(m \leq n)), 1_A \circ f \circ 1_V] & \textrm{(Associativity)} \\
&= [(f^{\mathcal{A}} \circ \Sigma(\alpha_n \circ \theta_n)) \circ \Sigma(D_V(m \leq n)), 1_A \circ f \circ 1_V] & \textrm{(Functoriality)} \\
&= [f^{\mathcal{A}} \circ (\Sigma(\alpha_n \circ \theta_n) \circ \Sigma(D_V(m \leq n))), 1_A \circ f \circ 1_V] & \textrm{(Associativity)} \\
&= [f^{\mathcal{A}} \circ \Sigma((\alpha_n \circ \theta_n) \circ D_V(m \leq n)), 1_A \circ f \circ 1_V] & \textrm{(Functoriality)} \\
&= [f^{\mathcal{A}} \circ \Sigma(\alpha_m \circ \theta_m), 1_A \circ f \circ 1_V] & \textrm{(Inductive Hypothesis)} \\
&= [f^{\mathcal{A}} \circ (\Sigma(\alpha_m) \circ \Sigma(\theta_m)), 1_A \circ f \circ 1_V] & \textrm{(Functoriality)} \\
&= [(f^{\mathcal{A}} \circ \Sigma(\alpha_m)) \circ \Sigma(\theta_m), 1_A \circ f \circ 1_V] & \textrm{(Associativity)} \\
&= [(f^{\mathcal{A}} \circ \Sigma(\alpha_m)) \circ \Sigma(\theta_m), 1_A \circ f] & \textrm{(Identity)} \\
&= [f^{\mathcal{A}} \circ \Sigma(\alpha_m), 1_A] \circ (\Sigma(\theta_m) + f) \\
&= \alpha_{m+1} \circ \theta_{m+1} & \textrm{(By definition)} \\
\end{align*}

Thus, \(A\) is the vertex of a cocone which induces the morphism \(\phi_f\). This morphism is a homomorphism, i.e., the following diagram commutes.

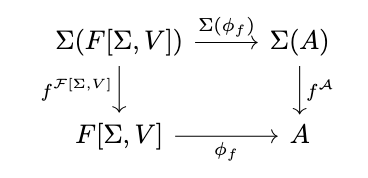
Next, consider the following diagram.

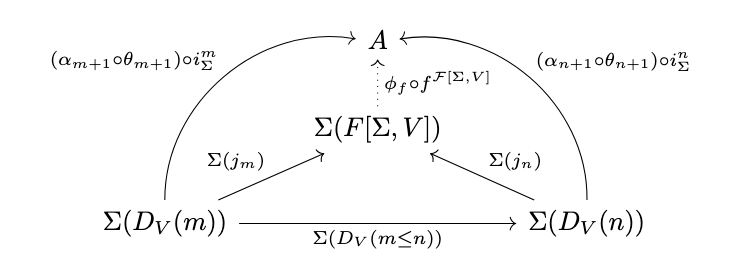
First, note that:

\begin{align*}
((\alpha_{n+1} \circ \theta_{n+1}) \circ i_\Sigma^n) \circ \Sigma(D_V(m \leq n)) &= (\alpha_{n+1} \circ \theta_{n+1}) \circ (i_\Sigma^n \circ \Sigma(D_V(m \leq n))) & \textrm{(Associativity)} \\
&= (\alpha_{n+1} \circ \theta_{n+1}) \circ (D_V(m+1 \leq n+1) \circ i_\Sigma^m) \\
&= ((\alpha_{n+1} \circ \theta_{n+1}) \circ D_V(m+1 \leq n+1)) \circ i_\Sigma^m & \textrm{(Associativity)} \\
&= (\alpha_{m+1} \circ \theta_{m+1}) \circ i_\Sigma^m & \textrm{(Previously Established)}
\end{align*}

Thus, these morphisms form a cocone and the mediating morphism must be unique. Then:

\begin{align*}
(\phi_f \circ f^{\mathcal{F}[\Sigma, V]}) \circ \Sigma(j_m) &= \phi_f \circ (f^{\mathcal{F}[\Sigma, V]} \circ \Sigma(j_m)) & \textrm{(Associativity)} \\
&= \phi_f \circ (j_{m+1} \circ i_\Sigma^m) & \textrm{(By definition of \(f^{\mathcal{F}[\Sigma, V]}\))} \\
&= (\phi_f \circ j_{m+1}) \circ i_\Sigma^m & \textrm{(Associativity)} \\
&= (\alpha_{m+1} \circ \theta_{m+1}) \circ i_\Sigma^m & \textrm{(By definition of \(\phi_f\))}
\end{align*}

Also:

\begin{align*}
(f^{\mathcal{A}} \circ \Sigma(\phi_f)) \circ \Sigma(j_m) &= f^{\mathcal{A}} \circ (\Sigma(\phi_f) \circ \Sigma(j_m)) & \textrm{(Associativity)} \\
&= f^{\mathcal{A}} \circ \Sigma(\phi_f \circ j_m) & \textrm{(Functoriality)} \\
&= f^{\mathcal{A}} \circ \Sigma(\alpha_m \circ \theta_m) & \textrm{(By definition of \(\phi_f\))} \\
&= f^{\mathcal{A}} \circ (\Sigma(\alpha_m) \circ \Sigma(\theta_m)) & \textrm{(Funtoriality)} \\
&= (f^{\mathcal{A}} \circ \Sigma(\alpha_m)) \circ \Sigma(\theta_m) & \textrm{(Associativity)} \\
&= ([f^{\mathcal{A}} \circ \Sigma(\alpha_m), 1_A] \circ (\Sigma(\theta_m) + f)) \circ i_\Sigma^m \\
&= (\alpha_{m+1} \circ \theta_{m+1}) \circ i_\Sigma^m & \textrm{(By definition of \(\alpha\) and \(\theta\))} \\
\end{align*}

Thus, \(\phi_f \circ f^{\mathcal{F}[\Sigma, V]} = f^{\mathcal{A}} \circ \Sigma(\phi_f)\) and \(\phi_f\) is a homomorphism.

Define \(\eta_V = j_0\) and consider the following diagram.

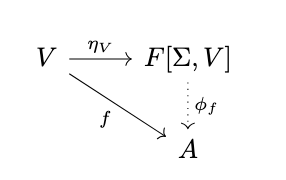
Note the following:

\begin{align*}
\phi_f \circ \eta_V &= \phi_f \circ j_0 & \textrm{(By definition of \(\eta_V\))} \\
&= \alpha_0 \circ \theta_0 & \textrm{(By definition of \(\phi_f\))} \\
& = 1_A \circ f & \textrm{(By definition of \(\alpha_0\), \(\theta_0\))} \\
& = f & \textrm{(Identity)}
\end{align*}

Finally, suppose that there exists another morphism \(\phi_f'\) such that \(\phi_f' \circ f^{\mathcal{F}[\Sigma, V]} = f^{\mathcal{A}} \circ G(\phi_f')\) and \(\phi_f' \circ \eta_V = f\). First, note that:

\begin{align*}
\phi_f' \circ j_0 &= \phi_f' \circ \eta_V & \textrm{(By definition of \(\eta_V\))} \\
&= f & \textrm{(By hypothesis)} \\
&= 1_A \circ f & \textrm{(Identity)} \\
&= \alpha_0 \circ \theta_0 & \textrm{(By definition of \(\alpha_0 \circ \theta_0\))}
\end{align*}

Next, suppose that \(\phi_f' \circ j_n = \alpha_n \circ \theta_n\), and note that:

\begin{align*}
\phi_f' \circ j_{n+1} &= [(\phi_f' \circ j_{n+1}) \circ i_\Sigma^n, (\phi_f' \circ j_{n+1}) \circ i_V^n] & \textrm{(By definition)} \\
&= [(\phi_f' \circ j_{n+1}) \circ i_\Sigma^n, \phi_f' \circ (j_{n+1} \circ i_V^n)] & \textrm{(Associativity)} \\
&= [(\phi_f' \circ j_{n+1}) \circ i_\Sigma^n, \phi_f' \circ (j_{n+1} \circ D_V(0 \leq n+1))] & \textrm{(By definition of \(D_V\))} \\
&= [(\phi_f' \circ j_{n+1}) \circ i_\Sigma^n, \phi_f' \circ j_0] & \textrm{(By definition of colimit)} \\
&= [(\phi_f' \circ j_{n+1}) \circ i_\Sigma^n, \phi_f' \circ \eta_V] & \textrm{(By definition of \(\eta_V\))} \\
&= [(\phi_f' \circ j_{n+1}) \circ i_\Sigma^n, f] & \textrm{(By hypothesis)} \\
&= [\phi_f' \circ (j_{n+1} \circ i_\Sigma^n), f] & \textrm{(Associativity)} \\
&= [\phi_f' \circ (f^{\mathcal{F}[\Sigma, V]} \circ \Sigma(j_n)), f] & \textrm{(Definition of \(f^{\mathcal{F}[\Sigma, V]}\))} \\
&= [(\phi_f' \circ (f^{\mathcal{F}[\Sigma, V]}) \circ \Sigma(j_n), f] & \textrm{(Associativity)} \\
&= [(f^{\mathcal{A}} \circ \Sigma(\phi_f')) \circ \Sigma(j_n), f] & \textrm{(By hypothesis)} \\
&= [f^{\mathcal{A}} \circ (\Sigma(\phi_f') \circ \Sigma(j_n)), f] & \textrm{(Associativity)} \\
&= [f^{\mathcal{A}} \circ \Sigma(\phi_f' \circ j_n), f] & \textrm{(Functoriality)} \\
&= [f^{\mathcal{A}} \circ \Sigma(\alpha_n \circ \theta_n), f] & \textrm{(Inductive Hypothesis)} \\
&= [f^{\mathcal{A}} \circ (\Sigma(\alpha_n) \circ \Sigma(\theta_n)), f] & \textrm{(Functoriality)} \\
&= [(f^{\mathcal{A}} \circ \Sigma(\alpha_n)) \circ \Sigma(\theta_n), f] & \textrm{(Associativity)} \\
&= [(f^{\mathcal{A}} \circ \Sigma(\alpha_n)) \circ \Sigma(\theta_n), 1_A \circ f] & \textrm{(Identity)} \\
&= [(f^{\mathcal{A}} \circ \Sigma(\alpha_n)), 1_A] \circ (\Sigma(\theta_n) + f) & \textrm{(By definition)} \\
&= \alpha_{n+1} \circ \theta_{n+1} & \textrm{(By definition of \(\alpha_{n+1}\) and \(\theta_{n+1}\))} \\
\end{align*}

Thus, by the definition of colimit, \(\phi_f' = \phi_f\). \(\square\)

Relations

Definition (Relation on an Object). A relation on an object \(A\) in a category \(\mathbb{C}\) is a subobject \(R\) of \(A \times A\), i.e. there exists a monomorphism \(i_R: R \hookrightarrow A \times A\). The relational projections are the morphisms \(\pi^R_1 = \pi_1 \circ i_R\) and \(\pi^R_2 = \pi_2 \circ i_R\).

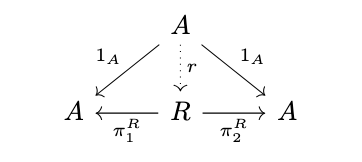
Definition (Reflexive Relation). A relation \(R\) on an object \(A\) is reflexive if there exists a morphism \(r : A \rightarrow R\) such that \(\pi^R_1 \circ r = 1_A\) and \(\pi^R_2 \circ r = 1_A\), i.e., the following diagram commutes.

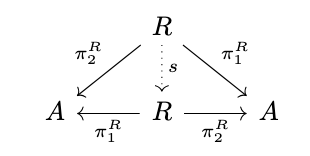
Definition (Symmetric Relation). A relation \(R\) on an object \(A\) is symmetric if there exists a morphism \(s : R \rightarrow R\) such that \(\pi^R_1 \circ s = \pi^R_2\) and \(\pi^R_2 \circ s = \pi^R_1\), i.e., the following diagram commutes.

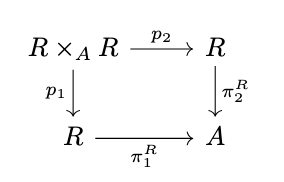
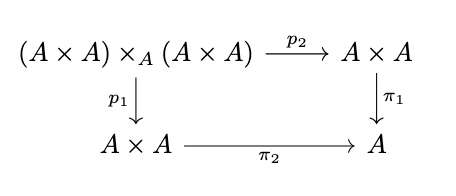
Definition (Transitive Relation). A relation \(R\) on an object \(A\) is transitive if there exists a morphism \(t : R \times_A R \rightarrow R\) (where \(R \times_A R\) is the pullback with projections \(p1\) and \(p2\) indicated in the following diagram

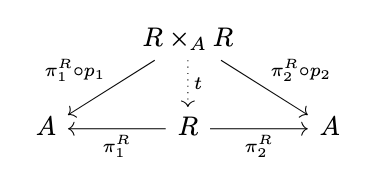
such that \(\pi^R_1 \circ t = \pi^R_1 \circ p_1\) and \(\pi^R_2 \circ t = \pi^R_2 \circ p_2\), i.e., the following diagram commutes.

Definition (Equivalence Relation). An equivalence relation is a reflexive, symmetric, transitive relation.

Congruences

Definition (Congruence). A congruence on a \(\Sigma\)-algebra \(\mathcal{A}\) is an equivalence relation \(R\) on \(A\) such that there exists a \(\Sigma\)-algebra \(\mathcal{R}\) with carrier \(R\) such that each of the relational projections is a homomorphism of algebras, i.e., the following diagram commutes.

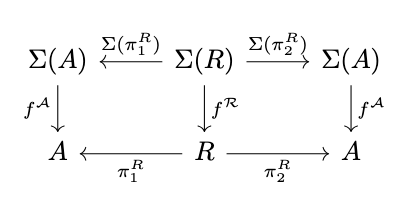
Definition (Fully Invariant Congruence). A congruence \(R\) on an algebra \(\mathcal{A}\) is fully invariant if for every endomorphism \(\phi\) on \(\mathcal{A}\) there exists a morphism \(f_{\phi} : R \rightarrow R\) such that \(\pi_1^R \circ f = \phi \circ \pi_1^R\) and \(\pi_2^R \circ f = \phi \circ \pi_2^R\), i.e., the following diagram commutes.

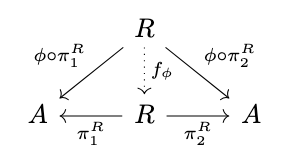
Alternatively, if the underlying category has exponential objects, then \(R\) is fully invariant if the following diagram commutes.

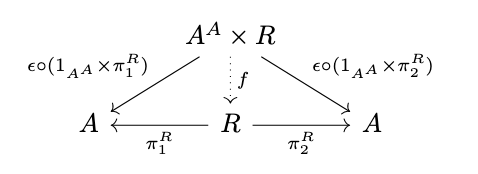
Theorem (Equivalence of Definitions for Fully Invariant Congruences). If the underlying category of an algebra \(\mathcal{A}\) also has a terminal object \(1\), then the definition of a fully invariant congruence \(R\) on \(A\) with exponential objects implies the definition without exponential objects.

Proof. Consider the following diagram for any endomorphism \(\phi : A \rightarrow A\).

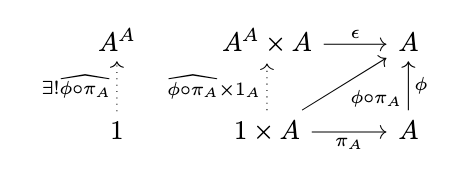
Since \(R\) is fully invariant, there exists a morphism \(f : A^A \times R \rightarrow R\) as in the diagram above. Define \(f_\phi = f \circ (\widehat{\phi \circ \pi_A} \times 1_A) \circ \langle !_R, 1_R \rangle\), as in the following diagram.

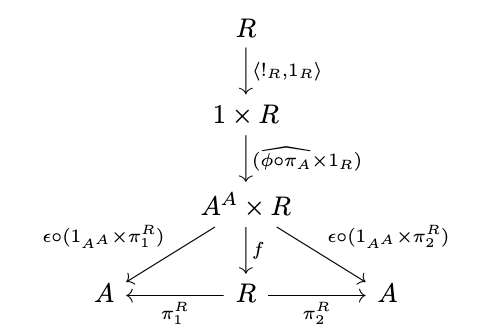
Now, consider the following:

\begin{align*}
\pi_1^R \circ f_{\phi} &= \pi_1^R \circ f \circ (\widehat{\phi \circ \pi_A} \times 1_R) \circ \langle !R, 1_R \rangle & \textrm{(By Definition)} \\
&= \epsilon \circ (1{A^A} \times \pi_1^R) \circ (\widehat{\phi \circ \pi_A} \times 1_R) \circ \langle !_R, 1_R \rangle & \textrm{(By Definition of \(f\))} \\
&= \epsilon \circ (\widehat{\phi \circ \pi_A} \times \pi_1^R) \circ \langle !_R, 1_R \rangle & \textrm{(Definition of Product)} \\
&= \epsilon \circ ((\widehat{\phi \circ \pi_A}) \times 1_A) \circ (!_1 \times \pi_1^R) \circ \langle !_R, 1_R \rangle & \textrm{(Definition of Product)} \\
&= \phi \circ \pi_A \circ (!_1 \times \pi_1^R) \circ \langle !_R, 1_R \rangle & \textrm{(Definition of \(\widehat{\phi \circ \pi_A}\))} \\
&= \phi \circ \pi_A \circ \langle !_R, \pi_1^R \rangle & \textrm{Definition of Product} \\
&= \phi \circ \pi_1^R & \textrm{Definition of \(\pi_A\)} \\
\end{align*}

Similar equations apply for \(\pi_2^R \circ f_{\phi}\). Thus, \(R\) is fully invariant according to the definition without exponential objects. \(\square\)

Closures

Definition (Closure Algebra). Given an algebra \(\mathcal{A}\), define the reflexive closure operation as \(\langle 1_A, 1_A \rangle\) as in the following diagram,

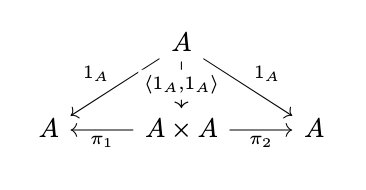
define the symmetric closure operation as \(\langle \pi_2, \pi_1 \rangle\) as in the following diagram,

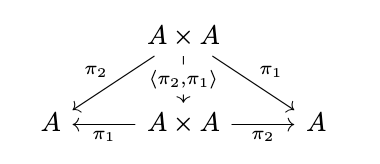
define the transitive closure operation as \(\langle \pi_2 \circ p_1, \pi_1 \circ p_2 \rangle\) as in the following diagram,

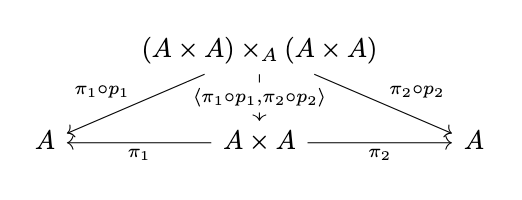
where the projections \(p_1\) and \(p_2\) are defined as in the following diagram,

and define the substitution closure operation as \(\langle \epsilon \circ (1_{A^A} \times \pi_1), \epsilon \circ (1_{A^A} \times \pi_2) \rangle\) as in the following diagram,

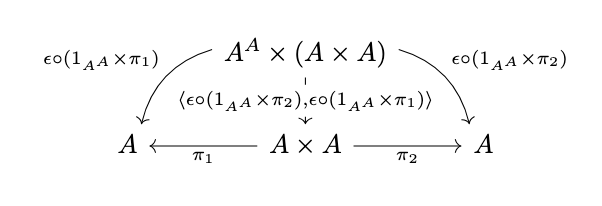
where \(\epsilon : A^A \times A \rightarrow A\) is the evaluation map of the exponential \(A^A\). Then, define the closure algebra as the algebra that extends \(\mathcal{A} \times \mathcal{A}\) by adjoining its operation \(f^{\mathcal{A}\times\mathcal{A}}\) to the closure operations just defined.

Theorem (Closure Algebras and Fully Invariant Congruences). A relation \(R\) on the carrier \(A\) of a \(\Sigma\)-algebra \(\mathcal{A}\) is a fully invariant congruence if and only if \(R\) carries a subalgebra of the closure algebra.

Proof. This is really a restatement of the definition of a fully invariant congruence; we verify the details here.

If \(R\) carries a subalgebra, then the following diagram commutes.

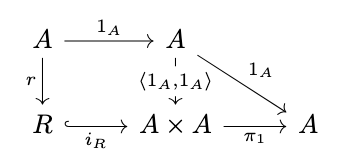
Then:

\begin{align*}
\pi^R_1 \circ r &= \pi_1 \circ i_r \circ r \\
&= \pi_1 \circ \langle 1_A, 1_A \rangle \circ 1_A \\
&= 1_A
\end{align*}

Likewise, \(\pi^R_2 \circ r = 1_A\) and \(R\) is thus reflexive. Conversely, if \(R\) is reflexive, then:

\begin{align*}
\pi_1 \circ i_R \circ r &= \pi^R_1 \circ r \\
&= 1_A \\
\end{align*}

Likewise, \(\pi_1 \circ i_R \circ r = 1_A\) and hence \(i_R \circ r = \langle 1_A, 1_A \rangle\) and \(R\) is a subalgebra. Similarly, if \(R\) carries a subalgebra, then the following diagram commutes.

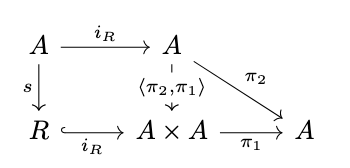
Then:

\begin{align*}
\pi^R_1 \circ s &= \pi_1 \circ i_R \circ s \\
&= pi_1 \circ \langle \pi_2, \pi_1 \rangle \circ i_R \\
&= \pi_1 \circ i_R \\
&= \pi^R_2
\end{align*}

Likewise, \(\pi^R_2 \circ s = \pi^R_1\) and so \(R\) is symmetric. Conversely, if \(R\) is symmetric, then:

\begin{align*}
\pi_1 \circ i_R \circ s &= \pi^R_1 \circ s \\
&= \pi^R_2 \\
&= \pi_2 \circ i_R \\
&= \pi_1 \circ \langle \pi_2, \pi_1 \rangle \circ i_R \\
&= \pi_1 \circ \langle \pi^R_2, \pi^R_1 \rangle \\
\end{align*}

Likewise, \(\pi_2 \circ i_R \circ s = \pi_2 \circ \langle \pi^R_2, \pi^R_1 \rangle\) and hence \(i_R \circ s = \langle \pi^R_2, \pi^R_1 \rangle = \langle \pi_2, \pi_1 \rangle \circ i_R\) and \(R\) is a subalgebra.

Next, if \(R\) carries a subalgebra, then the following diagram commutes.

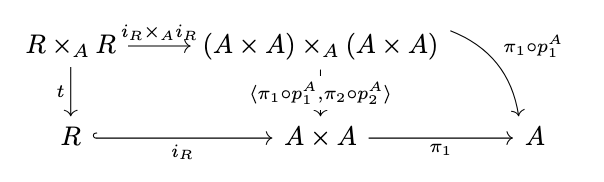
Then:

\begin{align*}
\pi^R_1 \circ t &= \pi_1 \circ i_R \circ t \\
&= \pi_1 \circ \langle \pi_1 \circ p^A_1, \pi_2 \circ pi^A_2 \rangle \circ (i_R \times_A i_R) \\
&= \pi_1 \circ p^A_1 \circ (i_R \times_A i_R) \\
&= \pi_1 \circ i_R \circ p^R_1 \\
&= \pi^R_1 \circ p^R_1
\end{align*}

Likewise, \(\pi^R_2 \circ t = \pi^R_2 \circ p^R_2\), so \(R\) is transitive. Conversely, if \(R\) is transitive, then:

\begin{align*}
\pi_1 \circ i_R \circ t &= \pi^R_1 \circ r \\
&= \pi^R_1 \circ p^R_1 \\
\end{align*}

Likewise, \(\pi_2 \circ i_R \circ t = \pi^R_2 \circ p^R_2\), hence \(i_r \circ t = \langle \pi^R_1 \circ p^R_1, \pi^R_2 \circ p^R_2 \rangle\). Then:

\begin{align*}
i_r \circ t &= \langle \pi^R_1 \circ p^R_1, \pi^R_2 \circ p^R_2 \rangle \\
&= \langle \pi_1 \circ i_R \circ p^R_1, \pi_2 \circ i_R \circ p^R_2 \rangle \\
&= \langle \pi_1 \circ p^A_1 \circ (i_R \times_A i_R), \pi_2 \circ p^A_2 \circ (i_R \times_A i_R) \rangle & (\textrm{See following diagram)} \\&= \langle \pi_1 \circ p^A_1, \pi_2 \circ p^A_2 \rangle \circ (i_R \times_A i_R)
\end{align*}

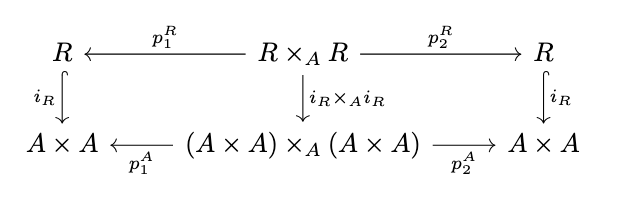
Thus, \(R\) is a subalgebra.

Next, if \(R\) carries a subalgebra, then the following diagram commutes.

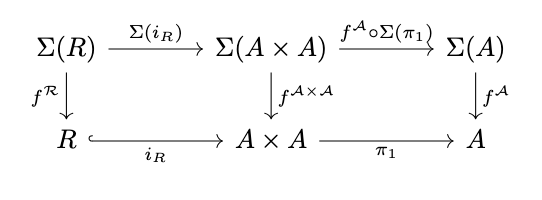
Then:

\begin{align*}
\pi^R_1 \circ f^{\mathcal{R}} &= \pi_1 \circ i_R \circ f^{\mathcal{R}} \\
&= \pi_1 \circ f^{\mathcal{A} \times \mathcal{A}} \circ \Sigma(i_R) \\
&= f^{\mathcal{A}} \circ \Sigma(\pi_1) \circ \Sigma(i_R) & \textrm{(By definition of \(f^{\mathcal{A} \times \mathcal{A}}\))} \\
&= f^{\mathcal{A}} \circ \Sigma(\pi_1 \circ i_R) \\
&= f^{\mathcal{A}} \circ \Sigma(\pi^R_1) \\
\end{align*}

Likewise, \(\pi^R_2 \circ f^{\mathcal{R}} = f^{\mathcal{A}} \circ \Sigma(\pi^R_2)\), hence \(i_R \circ f^{\mathcal{R}} = \langle f^{\mathcal{A}} \circ \Sigma(\pi^R_1), f^{\mathcal{A}} \circ \Sigma(\pi^R_2) \rangle\). Then:

\begin{align*}
i_R \circ f^{\mathcal{R}} &= \langle f^{\mathcal{A}} \circ \Sigma(\pi^R_1), f^{\mathcal{A}} \circ \Sigma(\pi^R_2) \rangle \\
&= \langle f^{\mathcal{A}} \circ \Sigma(\pi_1 \circ i_R), f^{\mathcal{A}} \circ \Sigma(\pi_2 \circ i_R) \rangle \\
&= \langle f^{\mathcal{A}} \circ \Sigma(\pi_1) \circ \Sigma(\circ i_R), f^{\mathcal{A}} \circ \Sigma(\pi_2) \circ \Sigma(\circ i_R) \rangle \\
&= \langle f^{\mathcal{A}} \circ \Sigma(\pi_1), f^{\mathcal{A}} \circ \Sigma(\pi_2) \rangle \circ \Sigma(i_R) \\
&= \langle \pi_1 \circ f^{\mathcal{A} \times \mathcal{A}}, \pi_2 \circ f^{\mathcal{A} \times \mathcal{A}} \circ \Sigma(i_R) \\
&= f^{\mathcal{A} \times \mathcal{A}} \circ \Sigma(i_R)
\end{align*}

Thus, \(R\) carries a subalgebra.

Next, suppose that \(R\) carries a subalgebra and consider the following diagram.

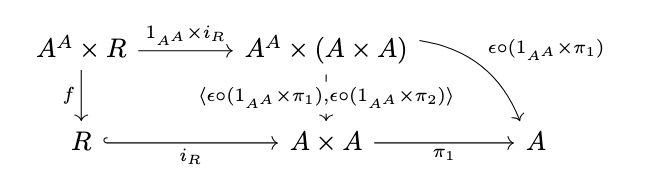
Then:

\begin{align*}\pi^R_1 \circ f &= \pi_1 \circ i_R \circ f \\&= \pi_1 \circ \langle \epsilon \circ (1_{A^A} \times \pi_1) {,} \epsilon \circ (1_{A^A} \times \pi_2) \rangle \circ (1_{A^A} \times i_R) \\ &= \epsilon \circ (1_{A^A} \times \pi_1) \circ (1_{A^A} \times i_R) \\  &= \epsilon \circ (1_{A^A} \times \pi^R_1) \end{align*}

Likewise, \(\pi^R_2 \circ f = \epsilon \circ (1_{A^A} \times \pi^R_2)\), and hence \(R\) is fully invariant.

Finally, suppose that \(R\) is fully invariant. Then:

\begin{align*}\pi_1 \circ i_R \circ f &= \pi^R_1 \circ f \\&= \epsilon \circ (1_{A^A} \times \pi^R_1)\end{align*}

Likewise, \(\pi_2 \circ i_R \circ f = \epsilon \circ (1_{A^A} \times \pi^R_2)\), hence \(i_R \circ f = \langle \epsilon \circ (1_{A^A} \times \pi^R_1), \epsilon \circ (1_{A^A} \times \pi^R_2) \rangle\). Then:

\begin{align*}i_R \circ f &= \langle \epsilon \circ (1_{A^A} \times \pi^R_1), \epsilon \circ (1_{A^A} \times \pi^R_2) \rangle \\&= \langle \epsilon \circ (1_{A^A} \times \pi_1) \circ (1_{A^A} \times i_R), \epsilon \circ (1_{A^A} \times \pi^R_2) \circ (1^{A^A} \times i_R) \rangle \\&= \langle \epsilon \circ (1_{A^A} \times \pi_1), \epsilon \circ (1_{A^A} \times \pi_2) \rangle \circ (1_{A^A} \times i_R)\end{align*}

Thus, \(R\) carries a subalgebra. \(\square\)

Quotient Algebras

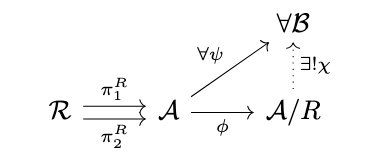
Definition (Quotient Algebra). The quotient algebra \(\mathcal{A}/R\) for a \(\Sigma\)-algebra \(\mathcal{A}\) and congruence \(R\) is the coequalizer of the relational projections in \(\Sigma\)-Alg, i.e., the following diagram commutes. The carrier is denoted \(A/R\) and the operation is denoted \(f^{\mathcal{A}/R}\).

Kernels

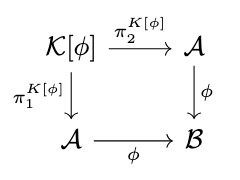
Definition (Kernel of a Homomorphism). The kernel of a homomorphism \(\phi : \mathcal{A} \rightarrow \mathcal{B}\) is the relation \(K[\phi]\) on \(A\) which carries the algebra \(\mathcal{K}[\phi]\) which is the pullback of \(\phi\) along itself as in the following diagram.

Theorem (Kernels are Congruences). Every kernel is a congruence.

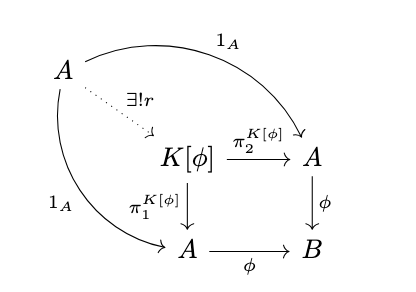
Proof. Since there is a pullback in \(\Sigma\)-Alg, there is likewise a pullback in the underlying category \(\mathbb{C}\). By the definition of a pullback, there exists a (unique) morphism \(r : A \rightarrow K[\phi]\) such that \(\pi^{K[\phi]}_1 \circ r = 1_A\) and \(\pi^{K[\phi]}_2 \circ r = 1_A\) as in the following diagram, thus the kernel is reflexive.

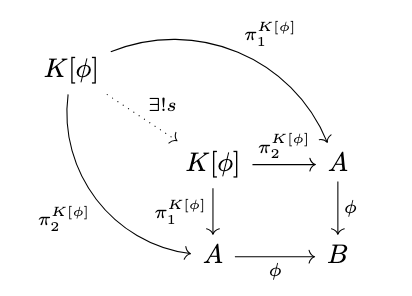
Likewise, there exists a (unique) morphism \(s : K[\phi] \rightarrow K[\phi]\) such that \(\pi^{K[\phi]}_1 \circ s = \pi^{K[\phi]}_2\) and \(\pi^{K[\phi]}_1 \circ s = \pi^{K[\phi]}_2\) as in the following diagram, thus the kernel is symmetric.

Similarly, given the pullback \(K[\phi] \times_A K[\phi]\) as in the following diagram,

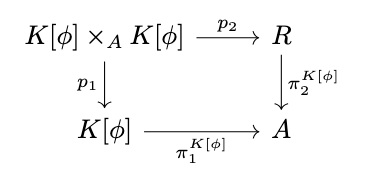
there exists a (unique) morphism \(t : K[\phi] \times_A K[\phi] \rightarrow K[\phi]\) such that \(\pi^{K[\phi]}_1 \circ t = \pi^{K[\phi]}_1 \circ p_1\) and \(\pi^{K[\phi]}_2 \circ t = \pi^{K[\phi]}_2 \circ p_2\) as in the following diagram, thus the kernel is transitive.

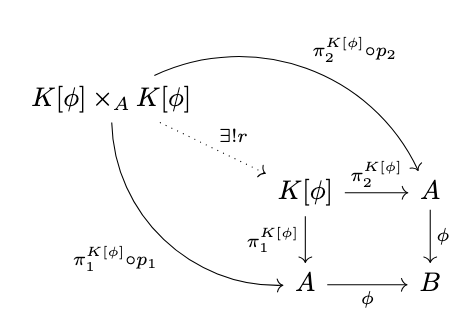
Finally, by definition, each of the relational projections is a homomorphism of algebras between \(\mathcal{K}\) and \(\mathcal{A}\), so the kernel is a congruence. \(\square\)

Lemma (Kernels and Monomorphisms). A homomorphism \(\phi : \mathcal{A} \rightarrow \mathcal{B}\) is a monomorphism if and only if the relational projections from its kernel \(K[\phi]\) are equal, i.e. \(\pi^{K[\phi]}_1 = \pi^{K[\phi]}_2\).

Proof. If \(\phi : \mathcal{A} \rightarrow \mathcal{B}\) is a monomorphism, then, since \(k[\phi]\) is the pullback of \(\phi\) along itself by definition, \(\phi \circ \pi^{K[\phi]}_1 = \phi \circ \pi^{K[\phi]}_2\) and thus, since \(\phi\) is a monomorphism, \(\pi^{K[\phi]}_1 = \pi^{K[\phi]}_2\).

Now, suppose that \(\pi^{K[\phi]}_1 = \pi^{K[\phi]}_2\), and consider any two parallel homomorphisms \(\psi_1 : \mathcal{C} \rightarrow \mathcal{A}\) and \(\psi_2 : \mathcal{C} \rightarrow \mathcal{A}\) such that \(\phi \circ \psi_1 = \phi \circ \psi_2\). Then, since \(K[\phi]\) is a pullback by definition, there exists a unique homomorphism \(\chi : C \rightarrow K[\phi]\) such that \(\pi_1 \circ \chi = \psi_1\) and \(\pi_2 \circ \chi = \psi_2\) as in the following diagram.

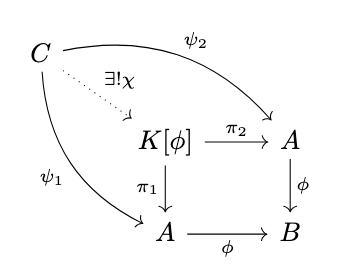
Since \(\pi_1 = \pi_2\), it then follows that:

\begin{align*}
\psi_1 &= \pi_1 \circ \chi \\
&= \pi_2 \circ \chi \\
&= \psi_2
\end{align*}

Thus, \(\phi\) is a monomorphism. \(\square\)

Lemma (Coequalizers and Epimorphisms). The coequalizer \(e : B \rightarrow C\) of a pair of parallel morphisms \(f_1 : A \rightarrow B\) and \(f_2 : B \rightarrow C\) is an epimorphism in any category \(\mathbb{C}\).

Proof. Le \(g_1 : C \rightarrow D\) and \(g_2 : C \rightarrow D\) be any pair of parallel morphisms, and suppose that \(g_1 \circ e = g_2 \circ e\) as in the following diagram.

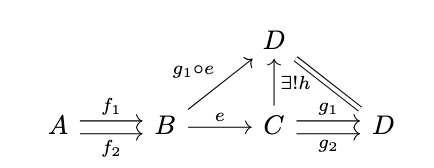
Then, since \(e \circ f_1 = e \circ f_2\) by definition, it follows that \((g_1 \circ e) \circ f_1 = (g_1 \circ e) \circ f_2\). Then, since \(e\) is a coequalizer, it follows that there exists a unique morphism \(h : C \rightarrow D\) such that \(h \circ e = g_1 \circ e\). However, \(g_2\) is a morphism such that \(g_2 \circ e = g_1 \circ e\), and thus, since such a morphism must be unique, it follows that \(g_1 = g_2\). Hence, \(e\) is an epimorphism. \(\square\)

Images

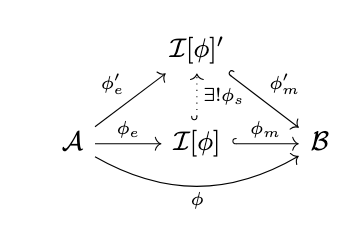
Definition (Image of a Homomorphism). The image of a homomorphism \(\phi : \mathcal{A} \rightarrow \mathcal{B}\) is the smallest subalgebra \(\mathcal{I}[\phi]\) through which \(\phi\) factors, i.e. there exists a homomorphism \(\phi_e : \mathcal{A} \rightarrow \mathcal{I}[\phi]\) and a monomorphism \(\phi_m : \mathcal{I}[\phi] \rightarrow B\) such that \(\phi = \phi_m \circ \phi_e\) and, for any other such subobject \(\mathcal{I}[\phi]'\) and factorization \(\phi_e' : \mathcal{A} \rightarrow \mathcal{I}[\phi]'\) and \(\phi_m : \mathcal{I}[\phi]' \rightarrow \mathcal{B}\), \(\mathcal{I}[\phi]\) is a subalgebra of \(\mathcal{I}[\phi]'\) as in the following diagram.

Preservation of Limits and Colimits

Theorem (Preservation of Limits). Consider any underlying category \(\mathbb{C}\) and any category of algebras \(\Sigma\)-\(\mathbf{Alg}\) for any signature \(\Sigma\) on \(\mathbb{C}\). A diagram \(D : \mathbb{I} \rightarrow \Sigma\textrm{-}\mathbf{Alg}\) has a limit if and only if the composite \(U \circ D\) with the forgetful functor \(U : \Sigma\textrm{-}\mathbf{Alg} \rightarrow \mathbb{C}\) has a limit.

Proof. Consider the following diagram in \(\mathbb{C}\).

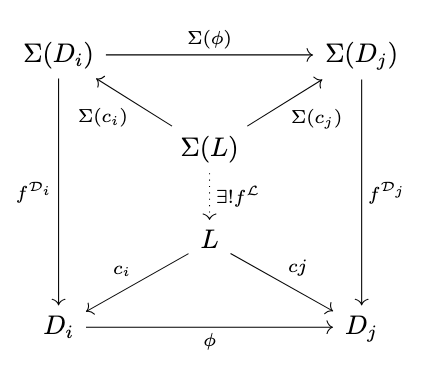
Suppose that the limit \(L\) of \(U \circ D\) exists in \(\mathbb{C}\). Note the following:

\begin{align*}
\phi \circ (f^{\mathcal{D}_i} \circ \Sigma(c_i)) &= (\phi \circ (f^{\mathcal{D}_i}) \circ \Sigma(c_i) & \textrm{(Associativity} \\
&= (f^{\mathcal{D}_j} \circ \Sigma(\phi)) \circ \Sigma(c_i) & \textrm{(\(\phi\) is a homomorphism)} \\
&= f^{\mathcal{D}_j} \circ (\Sigma(\phi) \circ \Sigma(c_i)) & \textrm{(Associativity)} \\
&= f^{\mathcal{D}_j} \circ \Sigma(c_j) & \textrm{(Functoriality)}
\end{align*}

Thus, there exists a cone with vertex \(\Sigma(L)\), and so there exists a unique morphism \(f^{\mathcal{L}} : \Sigma(L) \rightarrow L\) that makes the previous diagram commute. The \(\Sigma\)-algebra \(\mathcal{L}\) with carrier \(L\) and operation \(f^{\mathcal{L}}\) is the limit of the diagram \(D\) in \(\Sigma\)-Alg. (Further detail of proof omitted). \(\square\)

Theorem (Preservation of Colimits). Consider any underlying category \(\mathbb{C}\) and any category of algebras \(\Sigma\)-\(\mathbf{Alg}\) for a signature \(\Sigma\) on \(\mathbb{C}\) which preserves colimits of type \(\mathbb{I}\) for an index category \(\mathbb{I}\). A diagram \(D : \mathbb{I} \rightarrow \Sigma\textrm{-}\mathbf{Alg}\) has a colimit in \(\Sigma\)-**Alg** if and only if the composite \(U \circ D\) with the forgetful functor \(U : \Sigma\textrm{-}\mathbf{Alg} \rightarrow \mathbb{C}\) has a colimit.

Proof. Consider the following diagram.

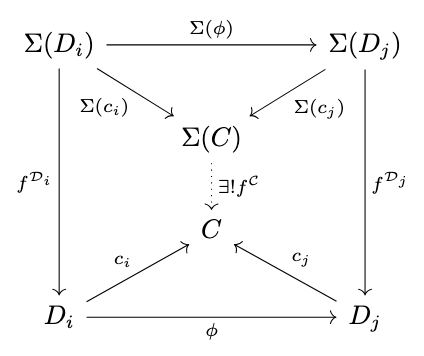
(Further details of proof omitted). \(\square\)

Regular Categories

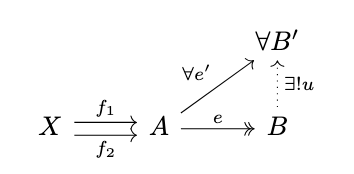
Definition (Regular Epimorphism). A regular epimorphism is an epimorphism \(e : A \rightarrow B\) in a category \(\mathbb{C}\) which is a coequalizer of \textit{some} pair of parallel morphisms, as in the following diagram.

Definition (Regular Category). A category is a regular category if:

• It admits all finite limits,
• Every kernel pair has a coequalizer,
• Regular epimorphisms are stable under pullback.

Theorem (Factorization Theorem). Every homomorphism whose underlying category \(\mathbb{C}\) is a regular category can be factored as an epimorphism followed by a monomorphism.

Proof. Let \(\phi : \mathcal{A} \rightarrow \mathcal{B}\) be any homomorphism and consider the following diagram.

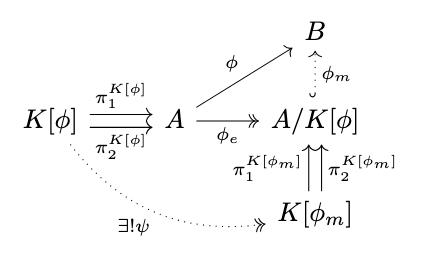
Since \(\mathbb{C}\) is regular, the kernel \(K[\phi]\) exists and admits a coequalizer \(\phi_e : A \rightarrow A/K[\phi]\) which is an epimorphism by the lemma above (coequalizers are epimorphisms). Since \(\phi \circ \pi^{K[\phi]}_1 = \phi \circ \pi^{K[\phi]}_2\) by definition of the kernel \(K[\phi]\) and \(\phi_e\) is a coequalizer, there exists a unique morphism \(\phi_m : A/K[\phi] \rightarrow B\) such that \(\phi = \phi_m \circ \phi_e\). Since \(\mathbb{C}\) is regular, the kernel \(K[\phi_m]\) exists and thus, since this kernel is a pullback, there exists a unique morphism \(\psi : K[\phi] \rightarrow K[\phi_m]\) such that \(\pi^{K[\phi_m]}_1 \circ \psi = \phi_e \circ \pi^{K[\phi]}_1\) and \(\pi^{K[\phi_m]}_2 \circ \psi = \phi_e \circ \pi^{K[\phi]}_2\). Then, since \(\phi_e \circ \pi^{K[\phi]}_1 = \phi_e \circ \pi^{K[\phi]}_2\), it follows that \(\pi^{K[\phi_m]}_1 \circ \psi = \pi^{K[\phi_m]}_2 \circ \psi\). Thus, it remains to show that \(\psi\) is an epimorphism, since, if so, then this implies that \(\pi^{K[\phi_m]}_1 = \pi^{K[\phi_m]}_2\), and thus, by the lemma above (kernels and monomorphisms), \(\phi_m\) is a monomorphism. Next, consider the following diagram.

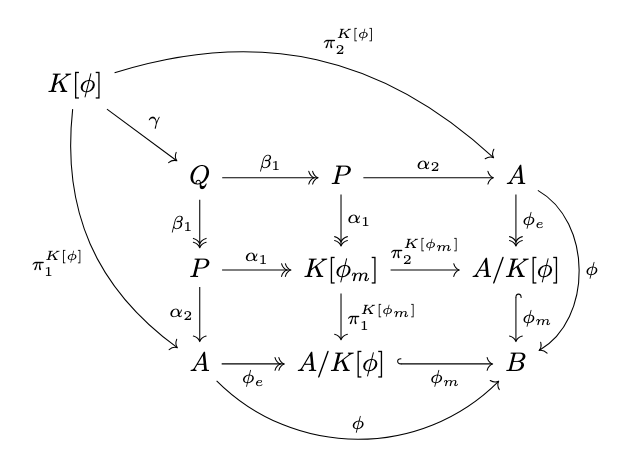
Since \(\phi_e\) is a regular epimorphism and \(\mathbb{C}\) is regular, the pullback \(\alpha_1\) is likewise a regular epimorphism. Then, again, the pullback of \(\alpha\) along itself is a regular epimorphism. Then, the previous diagram commutes, \(Q\) is the pullback of \(\phi\) along itself, so \(Q \cong K[\phi]\), and thus \(\alpha_1 \circ \beta_1 \circ \gamma = \psi\) since \(\psi\) is unique and thus \(\psi\) is an epimorphism. \(\square\)

Theorem (Canonical Image Theorem). For any homomorphism \(\phi : \mathcal{A} \rightarrow \mathcal{B}\) with an underlying category \(\mathbb{C}\) which is a regular category, the quotient algebra \(\mathcal{A}/K[\phi]\) is the image of \(\phi\).

Proof. Consider the following diagram.

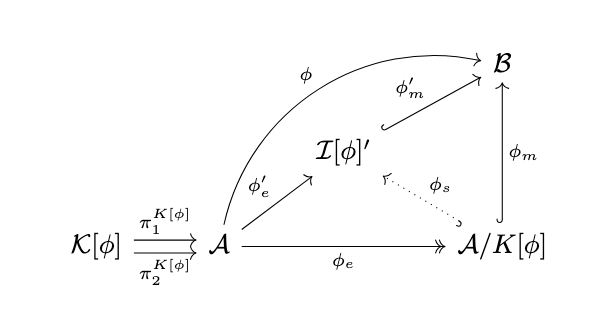
By the factorization theorem above, \(\phi\) can be factored as an epimorphism \(\phi_e : \mathcal{A} \rightarrow \mathcal{A}/K[\phi]\) followed by a monomorphism \(\phi_m: \mathcal{A}/K[\phi] \rightarrow \mathcal{B}\). Suppose that there exists an algebra \(\mathcal{I}[\phi]'\) and a factorization of \(\phi\) via homomorphisms \(\phi_e' : \mathcal{A} \rightarrow \mathcal{I}[\phi]'\) and \(\phi_m' : \mathcal{I}[\phi]' \hookrightarrow \mathcal{B}\) where \(\phi_m'\) is a monomorphism. Observe the following:

\begin{align*}
\phi_m' \circ (\phi_e' \circ \pi_1) &= (\phi_m' \circ \phi_e') \circ \pi_1 & \textrm{(Associativity)} \\
&= \phi \circ \pi_1 & \textrm{(Factorization)} \\
&= (\phi_m \circ \phi_e) \circ \pi_1 & \textrm{(Factorization)} \\
&= \phi_m \circ (\phi_e \circ \pi_1) & \textrm{(Associativity)} \\
&= \phi_m \circ (\phi_e \circ \pi_2) & \textrm{(Coequalizer)} \\
&= (\phi_m \circ \phi_e) \circ \pi_2 & \textrm{(Associativity)} \\
&= \phi \circ \pi_2 & \textrm{(Factorization)} \\
&= (\phi_m' \circ \phi_e') \circ \pi_2 & \textrm{(Factorization)} \\
&= \phi_m' \circ (\phi_e' \circ \pi_2) & \textrm{(Associativity)} \\
\end{align*}

Since \(\phi_m'\) is a monomorphism, it follows that \(\phi_e' \circ \pi_1 = \phi_e' \circ \pi_2\). Since \(\phi_e\) is an equalizer, there exists a unique morphism \(\phi_s : \mathcal{A}/K[\phi] \hookrightarrow \mathcal{I}[\phi]'\) such that \(\phi_s \circ \phi_e = \phi_e'\). Next, observe the following:

\begin{align*}
\phi_m \circ \phi_e &= \phi & \textrm{(Factorization)} \\
&= \phi_m' \circ \phi_e' & \textrm{(Factorization)} \\
&= \phi_m' \circ (\phi_s \circ \phi_e) & \textrm{(Previous Argument)} \\
&= (\phi_m' \circ \phi_s) \circ \phi_e & \textrm{(Associativity)} \\
\end{align*}

Thus, since \(\phi_e\) is an epimorphism, it follows that \(\phi_m = \phi_m' \circ \phi_s\). Finally, for any pair of parallel homomorphisms \(\psi_1, \psi_2 : \mathcal{C} \rightarrow \mathcal{A}/K[\phi]\) such that \(\phi_s \circ \psi_1 = \phi_s \circ \psi_2\) observe the following:

\begin{align*}
\phi_m \circ \psi_1 &= (\phi_m' \circ \phi_s) \circ \psi_1 & \textrm{(Previous Argument)} \\
&= \phi_m' \circ (\phi_s \circ \psi_1) & \textrm{(Associativity)} \\
&= \phi_m' \circ (\phi_s \circ \psi_2) & \textrm{(Hypothesis)} \\
&= (\phi_m' \circ \phi_s) \circ \psi_2 & \textrm{(Associativity)} \\
&= \phi_m \circ \psi_2 & \textrm{(Previous Argument)}
\end{align*}

Thus, since \(\phi_m\) is a monomorphism, it follows that \(\psi_1 = \psi_2\) and thus \(\phi_s\) is a monomorphism, so \(\mathcal{A}/K[\phi]\) is a subobject of \(\mathcal{I}[\phi]'\). \(\square\)

Homomorphism Theorem

Theorem (Homomorphism Theorem). For any regular epimorphism \(\phi: \mathcal{A} \rightarrow \mathcal{B}\) of \(\Sigma\)-algebras with an underlying regular category \(\mathbb{C}\), \(\mathcal{B} \cong \mathcal{A}/K[\phi]\).

Proof. Consider the following diagram in \(\mathbb{C}\).

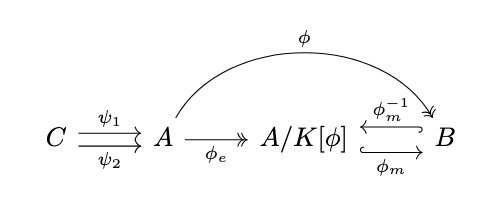
Since \(\phi\) is a regular epimorphism, it is, by definition, the coequalizer of some pair or parallel morphisms \(\psi_1, \psi_2 : C \rightarrow A\). By Theorem \ref{thm:factorization}, \(\phi\) factors as an epimorphism \(\phi_e\) followed by a monomorphism \(\phi_m\). Observe the following:

\begin{align*}\phi_m \circ (\phi_e \circ \psi_1) &= (\phi_m \circ \phi_e) \circ \psi_1 & \textrm{(Associativity)} \\    &= \phi \circ \psi_1 & \textrm{(Factorization)} \\    &= \phi \circ \psi_2 & \textrm{(Coequalizer)} \\    &= (\phi_m \circ \phi_e) \circ \psi_2 & \textrm{(Factorization)} \\    &= \phi_m \circ (\phi_e \circ \psi_2) & \textrm{(Associativity)} \end{align*}

Thus, since \(\phi_m\) is a monomorphism, it follows that \(\phi_e \circ \psi_1 = \phi_e \circ \psi_2\). Since \(\phi\) is a coequalizer, it follows that there exists a unique morphism \(\phi_m^{-1} : B \rightarrow A/K[\phi]\) such that \(\phi_m^{-1} \circ \phi = \phi_e\). Observe the following:

\begin{align*}(\phi_m^{-1} \circ \phi_m) \circ \phi_e &= \phi_m^{-1} \circ (\phi_m \circ \phi_e) & \textrm{(Associativity)} \\&= \phi_m^{-1} \circ \phi & \textrm{(Factorization)} \\    &= \phi_e & \textrm{(By Definition)} \end{align*}

Thus, since it is also the case that \(1_{A/K[\phi]} \circ \phi_e = \phi_e\) and \(\phi_e\) is an epimorphism, \(\phi_m^{-1} \circ \phi_m = 1_{A/K[\phi]}\). Likewise, consider the following:

\begin{align*}(\phi_m \circ \phi_m^{-1}) \circ \phi &= \phi_m \circ (\phi_m^{-1} \circ \phi) & \textrm{(Associativity)} \\ &= \phi_m \circ \phi_e & \textrm{(By Definition)} \\    &= \phi & \textrm{(Factorization)}\end{align*}

Thus, since it is also the case that \(1_B \circ \phi= \phi\) and \(\phi\) is an epimorphism, \(\phi_m \circ \phi_m^{-1} = 1_B\). Thus, \(B \cong A/K[\phi]\) in \(\mathbb{C}\). Now, since \(\phi_m\) is a homomorphism in \(\Sigma\)-Alg, it follows that \(\mathcal{B} \cong \mathcal{A}/K[\phi]\) in \(\Sigma\)-Alg. \(\square\)

Completions

Definition (Completion). For a category \(\mathbb{C}\) and a full subcategory \(\mathbb{D}\) with inclusion functor \(U : \mathbb{D} \rightarrow \mathbb{C}\), the completion of an object \(C\) of \(\mathbb{C}\) is the free object with respect to the functor \(U\), as in the following diagram;

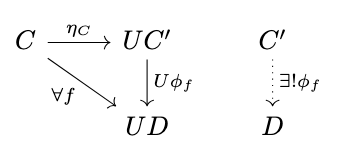
if there exists a completion for every object of \(\mathbb{C}\) if and only if the functor \(U\) has a left adjoint \(F\) as in the following diagram.

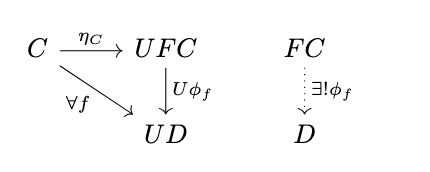
Definition (\(\mathbf{Rel}\) and \(\mathbf{Con}^+\)). For an object \(A\) of an underlying category \(\mathbb{C}\), the category \(\mathbf{Rel}_A\) consists of all relations on \(A\) as objects and inclusions (monomorphisms) as morphisms. The category \(\mathbf{Con}^+_A\) is the full subcategory of \(\mathbf{Rel}_A\) consisting of all fully invariant congruences on \(A\) as objects and inclusions as morphisms.

Definition (Fully Invariant Completion). For a relation \(R\) on an object \(A\) of a category \(\mathbb{C}\), the fully invariant completion of \(R\) is the completion (in the sense of definition \ref{def:completion}) with respect to the inclusion functor \(U : \mathbf{Con}^+_A \rightarrow \mathbf{Rel}_A\), i.e., the following diagram commutes.

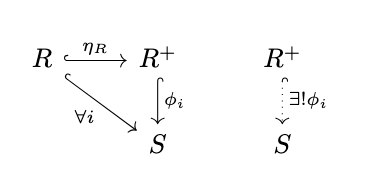
In detail, the completion, if it exists, is the fully invariant congruence \(R^+\) such that there exists an inclusion \(\eta_R : R \hookrightarrow R^+\) such that, for any inclusion \(i : R \hookrightarrow S\), there exists a unique inclusion \(\phi_i : R^+ \hookrightarrow S\) such that \(\phi_i \circ \eta_R = i\). If there exists a completion for each relation \(R\), then \(U\) has a left adjoint \(F : \mathbf{Rel}_A \rightarrow \mathbf{Con}^+_A\) with \(F(R) = R^+\) and \(F(i : R \hookrightarrow S) = i\). Thus, a fully invariant completion of a relation \(R\) is also the least fully invariant congruence containing \(R\) in the sense that \(R\) is the least subobject of \(R^+\).

Definition (Relation of Identities). A relation \(E\) on \(F[\Sigma, V]\) is called a relation of identities or relation of \(\Sigma\)-identities.

Models

Definition (Model, Satisfaction). A relation of identities \(E\) on \(F[\Sigma, V]\) is satisfied (or holds) in an algebra \(\mathcal{A}\) (written \(\mathcal{A} \models E\)) if, for every homomorphism \(\phi : \mathcal{F}[\Sigma, V] \rightarrow \mathcal{A}\), \(\phi \circ \pi^E_1 = \phi \circ \pi^E_2\), i.e., the following diagram commutes. The algebra \(\mathcal{A}\) is called a model of \(E\).

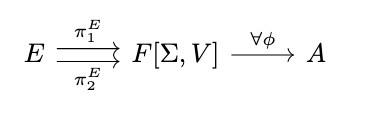
Equational Classes

Definition (Equational Class).

The category \(\mathbb{M}[E]\) of all models of a relation of identities \(E\) is called an equational class.